2.0. THE CONCEPT OF STRAIN

When a material undergoes stress, the material will also have some change in size. This change in size is referred to as deformation which is due to strain.

In contrast with stress as an invisible material characteristic, strain is a visible parameter seen when the material elongates or contracts.

                               

where:  
                 
               
                  deformation or change in length, m or in
            
                   original material length

2.1. STRESS-STRAIN DIAGRAM

The stress-strain diagram is the visual representation on what a material undergoes when a load is applied. The figure is the characteristic of steel under a certain load.

credits to Chicago Metal Rolled Products

At the start of the application, the stress is proportional to the strain until yield point. The elastic limit depicts that the material can get back to its original shape and size after the load is removed. After the yield point, the next stage is called, plastic limit. This condition prevents the material to get back to its original condition, contrary to the elastic limit.

2.2. HOOKE'S LAW

Hooke's Law states that in the elastic stage, the stress is proportional to the strain. This is where stress gets to be related with strain.

                                            

2.3. MODULUS OF ELASTICITY, E

From Hooke's law, another mathematician, named the slope of the proportionality relationship of the stress and strain. This slope has been named after him, Young's modulus, which was later known as the Modulus of Elasticity. The modulus of elasticity is a characteristic of every material, that is, each element has its own modulus of elasticity. For example, .

2.4. MODULUS OF RESILIENCE

The triangular area covered by the elastic limit is known as the modulus of resilience. The formula is:

                                          

And also if one is able to measure the characteristic area, from the elastic limit to the rupture point, that area is known as the modulus of toughness.

2.5. MECHANICAL STRAIN

Mechanical strain is the deformation due to an applied load. This uses the formula:

                 

where:
             

              mechanical deformation (deformation due to load)
         P =  load
         L =  original length
         A =  cross-sectional area
         E =   modulus of elasticity


EXAMPLE 2.5.1. DEFORMATION DUE TO A LOAD
EXAMPLE 2.5.2. LEAST DIAMETER TO COUNTER DEFORMATION
EXAMPLE 2.5.3. MECHANICAL STRAIN
EXAMPLE 2.5.4. MECHANICAL STRAIN
EXAMPLE 2.5.5. MECHANICAL STRAIN

         

2.6. THERMAL STRAIN

Thermal strain is the deformation due to the change in temperature. This is dependent on the materials coefficient of thermal expansion (coefficient of linear expansion, 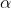. The formula states:

                

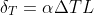
where:
               

          thermal deformation
       
               coefficient of thermal deformation
     
           change in temperature

          L = original length

EXAMPLE 2.6.1. THERMAL STRAIN: FREE EXPANSION
EXAMPLE 2.6.2. THERMAL STRAIN: FREE EXPANSION
EXAMPLE 2.6.3. THERMAL STRAIN: FREE EXPANSION

2.7. TOTAL STRAIN

The total strain is just the summation of the mechanical and the thermal strain.

                                  


EXAMPLE 2.7.1. TOTAL STRAIN: FREE EXPANSION
EXAMPLE 2.7.2. TOTAL STRAIN: FREE EXPANSION
EXAMPLE 2.7.3. DEFORMATION OF JOINED ELEMENTS
EXAMPLE 2.7.4. DEFORMATION OF JOINED ELEMENTS
EXAMPLE 2.7.5. DEFORMATION OF COMPOSITE ELEMENTS