INTERIOR BAYS: DESIGN FOR STRENGTH I POSITIVE FLEXURE - EXAMPLE

Using the previous example, determine the bar spacing for both the positive and negative moments in the interior bays using the following:

               Use:#25 bars

                     f'c   =  27.58 MPa
                     fy   =  413.69 MPa

   

To determine the properties of the rebar, check the values from the table below:

harrissupplysolutions.com

So with #25 bar: 

                       diameter = 25.4mm
                                 

DESIGN FOR STRENGTH I POSITIVE FLEXURE

Solve for the required area of steel,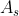 , and the required bar spacing is found as follows:

Effective depth (from previous computation) : 238mm

Solve for the required amount of reinforcing steel for a typical section with width b=1m. The formula for the nominal resistance is:

                                    

where the resistance force can be taken from the AASHTO table found in 5.5.4.2.1.

So,

                                                                                                                                                                    

From the general reinforced concrete design equations:

                                    

                               
                                  

Compare with :


                                 

Thus, use  .


The required are is then computed:

                             
                                  

The required bar spacing can be computed as follows:

                                 

CHECK FOR POSITIVE MOMENT FLEXURE CRACKING

For flexure, load factors considered are:

                         
                         

                          

                          


Compute for the positive service moment. Values for moments have already been previously computed.








AASHTO specifies  bar spacings (s) from the formula 5.7.3.4.-1


                      

in which

                     

where: 


  exposure factor
    =  1.0 for Class 1 exposure condition
    =  0.75 for Class 2 exposure condition

  thickness of concrete cover measured from extreme tension fiber to center of the flexural reinforcement located closest thereto (mm)

 tensile stress in steel reinforcement at the service limit state (MPa)

  overall thickness or depth of the component (mm)


So, using:

                  class I exposure condition:   

                     
                          

                          

for
                         


                         

where:
                       

                       

                       

                       

Therefore, for n = 8,
                 


                       

                      

So                 


From AASHTO 5.7.3.4.               

                        

                       


Compare the two spacing values. The selected spacing for strength 1 positive moment 500mm with 136mm. Thus the flexure cracking value should be used.

**OK for Service I positive moment in interior bays.