The area method is a shorter way in determining the shear and moment of beams; however, the procedures still entails the computation of the reactions. The process starts with the shear diagram considering the forces and reactions observed (depending on the kind of loading).
Pages
- Home
- ADVISING PROGRAM
- ADV MATH
- BLDG DESIGN 2
- BLDG DESIGN 2 LAB
- BRIDGE ENGG
- CE LAWS
- CONST MTRLS AND TESTING
- CONST MTRLS LAB
- CPM
- DYNAMICS
- ENGG SURVEYS
- ESTIMATES
- E. SURVEYING
- E. SURVEYING FIELD
- FLUID MECHANICS
- FLUID MECHANICS LAB
- HIGHWAY ENGG
- HYDRAULICS
- LATERAL LOADS ANALYSIS
- SANITARY ENGG
- STATICS
- STRENGTH OF MATERIALS
- TECHNICAL MECHANICS
- THEORY OF STRUCTURES
- TRANSPORTATION ENGG
Tuesday, 28 April 2020
EXAMPLE 2.7.1. OVERHANG DESIGN CASE 1
Using the previous example, design the deck overhang for the cast-in-place reinforced concrete deck. The parapet has been crash-tested and is deemed to have the capacity for the TL-4 load level.
[TL-4: Test Level Four: Taken to be generally acceptable for the majority of applications on high speed highways, freeways, expressways, and Interstate highways with a mixture of trucks and heavy vehicles.]
Materials used are the following:
Slab: Normal weight concrete, f'c = 27.58 MPa
fy = 413.69 MPa
Wearing surface: Asphalt concrete
Wearing surface: Asphalt concrete
Thickness of future wearing surface: 60mm
Thickness of top integral wearing surface: 12mm
DECK OVERHANG THICKNESS. AASHTO 13.7.3.1.2 specifies the minimum thickness according to different conditions:
- 200mm for concrete deck overhangs supporting a deck-mounted post system
- 300mm for side-mounted post system
- 200mm for concrete deck overhangs supporting concrete parapets or barriers
PARAPET PARAMETERS
BRIDGE RAILING PROPERTIES
The railing would need to be divided into portions for moment capacity calculations.
6.0 TRAVERSING
Traversing is the process of identifying the area of a given lot. All the different previous parameters discussed would have to be incorporated in this application in order to have a complete set of information before transferring information in the office.
5.0 COMPASS MEASUREMENT OF ANGLES AND DIRECTIONS
Another set of data that would have to be taken from the field is that for angles and directions. Although some total stations are able to determine the angles and directions of sights as well, the other older version of levels is inhibited.
There is a big difference in using bearings with the azimuths in surveying but they can be used interchangeably according to the surveyors' discretion.
4.0 VERTICAL DISTANCE MEASUREMENTS
Pacing and taping are used to measure horizontal distances, however, they are impossible to use for measuring elevations, thus, surveyors use levels. There are different levels used from a few decades ago until the evolution of digitized instruments used today, which not only measure vertical but also horizontal distances all in one shot.
Saturday, 25 April 2020
OVERHANG: REINFORCED CONCRETE DECK DESIGN
The design of overhang does not only consider dead and live loads on the interior bays but also load in case of truck collision.
AASHTO specification for overhang design includes:
AASHTO specification for overhang design includes:
- Design Case 1 (Extreme Event II) for horizontal force due to truck collision to the railing
- Design Case 2 (Extreme Event II) for vertical force due to truck collision to the railing
- Design Case 3 (Strength I) for the dead load and vehicular live loads to the overhang.
EXAMPLE 2.7.1. OVERHANG DESIGN CASE 1
EXAMPLE 2.7.2. OVERHANG DESIGN CASES 2 AND 3 AND OTHER CASES
EMPIRICAL DESIGN METHOD
The traditional design assumes that failure will occur in flexure, however, field and laboratory tests show that the ultimate strength of the concrete deck is controlled by its capacity to resist punching shear. This is the observation for empirical method.
When using the empirical deck design method, take note that it is only applicable to interior bays but not the overhang.
For the previous example:
Materials used are the following:
Slab: Normal weight concrete, f'c = 35 MPa
Wearing surface: Asphalt concrete
Thickness of future wearing surface: 60mm
Thickness of top integral wearing surface: 12mm
Traffic barriers are composite to the deck, and the deck is composite to the steel beams.
Full-depth diaphragms are used at the ends of the span.
There is no skew.
EFFECTIVE LENGTH
Assuming that you are going to use W250x200x67.
Properties are as follows: depth, h=257mm
width, w=204mm
web thickness = 8.9mm
CHECK DESIGN CONDITIONS
AASHTO 9.7.2.4 specifies the design conditions for empirical deck design method, the designer only needs to check if the project is OK with the following requirements:
- Cross-frames or diaphragms are used throughout the cross-section at lines of support.
- For cross-section involving torsionally stiff units, such as individual separated box beams, either intermediate diaphragms between eh boxes are provided at a spacing not to exceed 8000nn, or the need for supplemental reinforcement over the webs to accommodate transverse bending between the box units is investigated and reinforcement is provided if necessary.
- The supporting components are made of steel and/or concrete.
- The deck is fully cast-in-place and water cured.
- The deck is of uniform depth, except for haunches at girder flanges and other local thickening.
- The ratio of effective length to design depth does not exceed 18.0 and is not less than 6.0.
- Core depth of the slab is not less than 100mm.
- The effective length does not exceed 4100mm.
- The minimum depth of the slab is not less than 175mm, excluding a sacrificial wearing surface where applicable.
- There is an overhang beyond the centerline of the outside girder of at least 5.0 times the depth of the slab; this condition is satisfied if the overhang is at least 3.0 times the depth of the slab and a structurally continuous concrete barrier is made composite with the overhang.
- The specified 28-day strength of the deck concrete is not less than 28.0 MPa.
- The deck is made composite with the supporting structural components.
*A minimum of two shear connectors at 600-mm centers shall be provided in the negative moment region of continuous steel superstructures.
SELECT STEEL REINFORCEMENT
For the empirical deck design method, four layers fo isotropic reinforcement shall be provided according to AASHTO 9.7.2.5.The minimum amount of reinforcement shall be:
* Reinforcing steel shall be Grade 420 (Grade 60) or better.
* Spacing of steel shall not exceed 450mm.
* All reinforcement shall be straight bars, except the hooks.
Assuming D25mm reinforcing bars for both bottom longitudinal and transverse directions.
Use 450mm
Assuming D20mm reinforcing bars for both top longitudinal and transverse directions.
Use 450mm
Friday, 24 April 2020
DESIGN FOR LONGITUDINAL REINFORCEMENT
BOTTOM LONGITUDINAL REINFORCEMENT
AASHTO 9.7.3.2 specifies the formula when designing bottom longitudinal reinforcement:
- For primary reinforcement perpendicular to traffic:
- For primary reinforcement perpendicular to traffic:
where S = the effective span length taken as equal to the effective length, (mm)
TOP LONGITUDINAL REINFORCEMENT
The top longitudinal reinforcement focuses near concrete surfaces exposed to temperature changes for shrinkage and temperature stresses.
AASHTO 5.10.8 provides the condition to follow for top longitudinal reinforcement
where:
b = least width of component section (mm)
h = least thickness of component section (mm)
In addition, the maximum spacing of temperature and shrinkage reinforcement must be the smaller of 3 times the deck thickness.
INTERIOR BAYS: STRENGTH ONE DESIGN FOR NEGATIVE LIVE LOAD EFFECT
After determining the reinforcement used for positive moments, move further in determining the effect of negative live load.
Using the same S, the next thing you would need to consider is the flange width of the beam.
Assuming that you are going to use W250x200x67.
Properties are as follows: depth, h=257mm
width, w=204mm
web thickness = 8.9mm
The negative moment will be taken from the tip of the flange or 1/2 of the top flange width, which is 100mm for the specified W section. By interpolation, we would be able to identify the value.
s= 2650mm
distance from CL = 100mm
at s=2600: 26470 (@75mm) and 22730 (@150mm)
interpolate for 100mm,
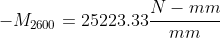
at s=2700: 26920 (@75mm) and 23170 (@150mm)
interpolate again for 100mm,
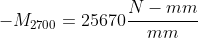
Then the negative moment due to live load:

Assume #19 bars:
Diameter = 20mm
Area = 284 sqmm
The procedure in determining the spacing of rebars will be the same:
1.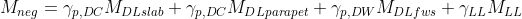
2. From the assumed bar size for thee negative moment. solve the area of steel and then the depth.
-t_{IWS})
3.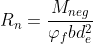
4.![\rho =0.85\left ( \frac{f'c}{fy} \right )\left [ 1-\sqrt{1-\frac{2R_{n}}{0.85f'c}} \right ]](https://latex.codecogs.com/gif.latex?\rho&space;=0.85\left&space;(&space;\frac{f'c}{fy}&space;\right&space;)\left&space;[&space;1-\sqrt{1-\frac{2R_{n}}{0.85f'c}}&space;\right&space;])
5.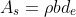
6.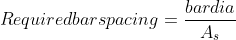
2.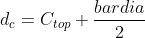
3.})
4.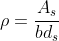
5. Using n=8
^{2}+2\rho&space;n}-\rho&space;n)
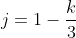
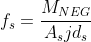

The procedure will be similar only that you are going to use the negative moment instead of the positive moment. The other thing you might be changing is the different diameter of the reinforcing bar you might be using.
For the negative moment, using the AASHTO table:
Using the same S, the next thing you would need to consider is the flange width of the beam.
Assuming that you are going to use W250x200x67.
Properties are as follows: depth, h=257mm
width, w=204mm
web thickness = 8.9mm
The negative moment will be taken from the tip of the flange or 1/2 of the top flange width, which is 100mm for the specified W section. By interpolation, we would be able to identify the value.
s= 2650mm
distance from CL = 100mm
at s=2600: 26470 (@75mm) and 22730 (@150mm)
interpolate for 100mm,
at s=2700: 26920 (@75mm) and 23170 (@150mm)
interpolate again for 100mm,
Then the negative moment due to live load:
Assume #19 bars:
Diameter = 20mm
Area = 284 sqmm
The procedure in determining the spacing of rebars will be the same:
1.
2. From the assumed bar size for thee negative moment. solve the area of steel and then the depth.
3.
4.
5.
6.
SERVICE I LIMIT STATE - NEGATIVE-MOMENT FLEXURE CRACKING
2.
3.
4.
5. Using n=8
Subscribe to:
Comments (Atom)







