EXAMPLE 4.2.1: CROSS PRODUCT: SHORTEST DISTANCE BETWEEN A POINT AND A LINE

Determine the shortest distance from point O to cable AC.

The shortest distance from the point of origin O to line AC is the perpendicular distance. Designating angle OAC as , we can create a triangle to determine the perpendicular distance d. Trigonometrically, the perpendicular distance d can be solved by: 

                                                          

With the forces being spatial, distances of the forces can vary from trigonometric solutions. But take note that the cross product of two vectors also involve their 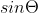. From the geometric definition of cross product:

                                     

                                                

By taking the scalar quantity only

                                                 

Considering d   from trigonometry

                                            

So, we can start solving for the parameters. Let's start with the coordinates of the points considered.

POINTS	i, ft	j, ft	k, ft
A	0	6	2
C	5cos60=2.5	0	5sin60=4.33
O	0	0	0

With force AC:

For the scalar of Force AC:





With force OA:






Take the cross product of both vectors AC and OA:










We only need to take the scalar of the cross product.




From the working equation for the shortest distance:


       ANSWER


Back to 4.2. INTRODUCTION TO CROSS PRODUCT