EXAMPLE 3.2.2: RESULTANT OF SPATIAL FORCES

The rope attached to the walls at points A and B is pulled by a man exerting 70 lb. Express force FA and FC as Cartesian vectors. Determine the magnitude and coordinate direction angles of the resultant force acting at B.

With the exerted force of the man = 70lb, both 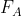 and . It would be easier to determine the forces' Cartesian vectors if you can determine the coordinates of the points included.

POINT	i, ft	j, ft	k, ft
A	5.00	7.00	5.00
B	-1.00	5.00	8.00
C	5.00	7.00	4.00

FOR FORCE FA

Determine the Cartesian vector of Force FA by taking the difference of points A and B's coordinates. Take the convention sign of the axes to identify if you are to use + or - in the equation.

At x-axis, for i: 5 - (-1) = 6ft (the force direction going to +x) thus +6i

At y-axis, for j:-7-(-5)   = -2ft (the force directing to -y) thus -2j

At z-axis, for k: 8- 5     = 3 ft (the force going downwards) thus -3k

Giving us the vector

The scalar of which is

So, the Cartesian vector of FA:



                              ANSWER

FOR FORCE FC

Similar with FA,





For which the scalar of FC becomes:



Then, the Cartesian vector of FC is







RESULTANT

MAGNITUDE:

FORCE	i	j	k
FA	60.00	-20.00	-30.00
FC	30.00	60.00	-20.00
summation	90.00	40.00	-50.00

                                                                   

                                           ANSWER


INCLINATION:





                                                    ANSWER


Back to COMPONENTS OF SPATIAL FORCES

EXAMPLE 3.2.1: RESULTANT OF SPATIAL FORCES

Shown is a bracket subjected to two forces. Express each force in Cartesian vector form and then determine the resultant force FR. Identify the magnitude and coordinate direction angles of the resultant force.

To take the resultant of spatial forces such as this problem, we should start working with each force's Cartesian representation or its -i, -j, -k form. In order to do this, observe that what were given in the problem are angles and not distances. This means that instead of taking note of the points' coordinates, we should use trigonometric functions to find the components.

FOR FORCE F1

Force F1 with a magnitude of 250N is inclined in the x-y axis at  and from that plane it was inclined down at . So if we take the vertical plane which would show xy as the horizontal and -z as the vertical we can compute for the component of F1 in the z-axis and xy-axis.

The z-component is already determined. The next thing to do is to break down Fxy into components x and y to complete the Cartesian vector form of force F1.

Fxy is then considered as the resultant force if we are going to look at the x-y plane. So we compute for the components








So, F1 in vector form is as follows:





FOR FORCE F2

If you take a closer look at force F2, you will notice that the force has angles given in the -x, -y, and -z axes already. So this would make the computation of the components easier than that of Force F1.








So F2 in vector form is




THE RESULTANT FORCE

Similar with 2D forces, the resultant force is computed by taking the summation of the components and utilizing the Pythagorean theorem. So,


 

FORCE	i	j	k
F1	86.547	185.601	-143.394
F2	-200	282.85	200
summation	-113.453	468.451	56.606

Using Pythagorean theorem, we will be able to solve for the magnitude of the resultant

                    ANSWER

In order to solve for the direction coordinate angles, use the principle of unit vector.






                                    ANSWER



Back to COMPONENTS OF SPATIAL FORCES

EXAMPLE 4.2.1: CROSS PRODUCT: SHORTEST DISTANCE BETWEEN A POINT AND A LINE

Determine the shortest distance from point O to cable AC.

The shortest distance from the point of origin O to line AC is the perpendicular distance. Designating angle OAC as , we can create a triangle to determine the perpendicular distance d. Trigonometrically, the perpendicular distance d can be solved by: 

                                                          

With the forces being spatial, distances of the forces can vary from trigonometric solutions. But take note that the cross product of two vectors also involve their . From the geometric definition of cross product:

                                     

                                                

By taking the scalar quantity only

                                                 

Considering d   from trigonometry

                                            

So, we can start solving for the parameters. Let's start with the coordinates of the points considered.

POINTS	i, ft	j, ft	k, ft
A	0	6	2
C	5cos60=2.5	0	5sin60=4.33
O	0	0	0

With force AC:

For the scalar of Force AC:





With force OA:






Take the cross product of both vectors AC and OA:










We only need to take the scalar of the cross product.




From the working equation for the shortest distance:


       ANSWER


Back to 4.2. INTRODUCTION TO CROSS PRODUCT