PROBLEM: Continuing Problem 1-1, assuming the columns are oriented as shown, determine the total shear force carried by each frame in the Roof Deck. Rectangular columns [400x600mm] and circular columns [500mm diamter].
SOLUTION:
Roof deck shear to be distributed: 235.21 kN
Compute for the moments of inertia of the columns.
Circular column: 
}{64}=3.07x10^{-3}) Vertical column [400x600mm(LxW)]:
Vertical column [400x600mm(LxW)]:
}{12}=7.20x10^{-3})
}{12}=3.20x10^{-3}) Horizontal column [600x400mm(LxW)]:
Horizontal column [600x400mm(LxW)]:
}{12}=3.20x10^{-3})
}{12}=7.20x10^{-3}) A. For Y-Frames [A-B-C-D-E]
1. Computing for ksy.
A. For Y-Frames [A-B-C-D-E]
1. Computing for ksy.  For Frame A:
For Frame A:  Frame B:
Frame B: =9.60x10^{-3}) Frame C:
Frame C: =9.34x10^{-3}) Frame D:
Frame D: =21.60x10^{-3}) Frame E:
Frame E:  2. For direct shear, take the summation of ksy to proceed to the percentage of ksy column.
2. For direct shear, take the summation of ksy to proceed to the percentage of ksy column.





 3. Direct shear,
3. Direct shear, )
=54.44kN)
=29.92kN)
=29.11kN)
=67.31kN)
=54.44kN)
| Y-frames | ksy x 10-3 | %ksy | Vd |
|---|
| A | 17.47 | 0.23 | 54.44 |
| B | 9.6 | 0.13 | 29.92 |
| C | 9.34 | 0.12 | 29.11 |
| D | 21.6 | 0.29 | 67.31 |
| E | 17.47 | 0.23 | 54.44 |
| 75.48 | 1 | 235.21 |
4. For torsional shear, a longer procedure is required starting with the location of the center of rigidity in the x-axis. Using the stiffness of columns, one can compute for the center of rigidity location in the x direction.
)
\left&space;(&space;9.60*4&space;\right&space;)\left&space;(&space;9.34*9&space;\right&space;)\left&space;(&space;21.6*15&space;\right&space;)\left&space;(&space;17.47*21&space;\right&space;)}{75.48}=10.78m) from Fr. A
from Fr. A
5. Eccentricity is computed as the difference between the center of rigidity located at 10.78m with the center of gravity (L/2).
\right&space;|)
&space;\right&space;|=0.28m)
6. As per code, the standard eccentricity adopted is equal to the eccentricity and 5% of the length in the direction analyzed.

=1.33m) 7. With eccentricity known, the torsion (Moment) is determined.
7. With eccentricity known, the torsion (Moment) is determined.
)
=312.83kN-m) 8. From the table, C is the distance of the frame to Crx.
8. From the table, C is the distance of the frame to Crx.




 9. Consider using the leftmost frame as the reference to solve for
9. Consider using the leftmost frame as the reference to solve for 
.
Thus,




 10.
10. )
=17.47x10^{-3})
=6.038x10^{-3})
=1.542x10^{-3})
=8.456x10^{-3})
=16.562x10^{-3}) 11.
11. )
=0.188)
=0.041)
=0.003)
=0.036)
=0.169) 12. Take summation of M' and solve for %M.
12. Take summation of M' and solve for %M.





 13.
13. )
=134.828kN-m)
=29.308kN-m)
=1.965kN-m)
=25.546kN-m)
=121.183kN-m)
14.






| Y-frames | Vd | Vt | Vtot |
|---|
| A | 54.44 | 12.51 | 66.95 |
| B | 29.92 | 4.32 | 34.24 |
| C | 29.11 | 1.10 | 30.21 |
| D | 67.31 | disregard | 67.31 |
| E | 54.44 | disregard | 54.44 |
B. For X-frames [1-2-3-4]
| X-frames | ksx x 10-3 | %ksx | Vdx |
|---|
| 3 | 24.00 | 0.38 | 88.93 |
| 2 | 19.61 | 0.31 | 72.66 |
| 1 | 19.87 | 0.31 | 73.62 |
| Σ | 63.48 | 1.00 | 235.21 |
\left&space;(&space;19.61*5&space;\right&space;)\left&space;(&space;24*9&space;\right&space;)}{63.48}=4.95m) [from frame 1]
[from frame 1]

=0.90m) Thus:
Thus:
=211.689kN-m)
| X-frames | ksx x 10-3 | c | c/c1 | ksx' | M' | %M | Applied M | Vtx |
|---|
| 3 | 24.00 | 4.05 | 0.82 | 19.636 | 0.080 | 0.447 | 94.635 | 23.37 |
| 2 | 19.61 | 0.05 | 0.01 | 0.198 | 0.000 | 0.000 | 0.012 | 0.24 |
| 1 | 19.87 | 4.95 | 1.00 | 19.870 | 0.098 | 0.553 | 117.042 | 23.64 |
| Σ | 63.48 | | | | 0.178 | 1.000 | 211.689 | |
| X-frames | Vd | Vt | Vtot |
|---|
| 3 | 88.93 | 23.37 | 112.29 |
| 2 | 72.66 | disregard | 72.66 |
| 1 | 73.62 | disregard | 73.62 |
| 235.21 | | |
 which in units
which in units 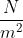 . This pressure (distributed load) is still to be converted into a force in order to be applied in the frame, thus
. This pressure (distributed load) is still to be converted into a force in order to be applied in the frame, thus  will then be multiplied with an area,
will then be multiplied with an area, 

